Advanced tutorial

In this tutorial, we demonstrate advanced use of the ChangepointInference package. Installation instructions are provided here.

First load the package:

require(ChangepointInference)
## Loading required package: ChangepointInference

To illustrate the software, we generate a synthetic dataset according to

and assume that $\mu_1,\ldots,\mu_T$ is piecewise constant, in the sense that $\mu_{\tau_j+1}=\mu_{\tau_j + 2 } = \ldots = \mu_{\tau_{j+1}}$, $\mu_{\tau_{j+1}} \neq \mu_{\tau_{j+1}+1}$, for $j=0,\ldots,K-1$, where $0 = \tau_{0} < \tau_{1} < \ldots < \tau_{K} < \tau_{K+1} = T$, and where $\tau_1,\ldots,\tau_K$ represent the true changepoints.

set.seed(1)
mu <- rep(c(1, 3, -2), each = 100)
dat <- mu + rnorm(length(mu))
plot(dat, cex = 1, ylab = "y", xlab = "t")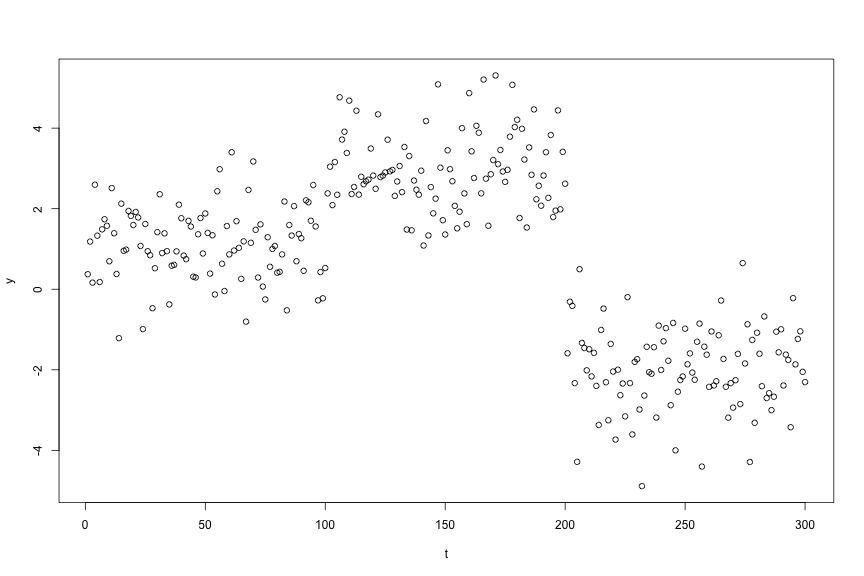

plot of chunk unnamed-chunk-2

Changepoint estimation

To estimate changepoints via $\ell_0$ segmentation, we use functional recursions (Rigaill, 2015; Maidstone, Hocking, Rigaill, & Fearnhead, 2017). In this section, we briefly describe these recursions and illustrate how this information can be extracted from our software.

Let $\mathrm{Cost}(y_{1:s}; u)$ be the cost of segmenting $y_{1:s}$ with $\mu_{s} = u$. Then $\mathrm{Cost}(y_{1:s}; u)$ can be efficiently computed: At the first timepoint, we have $\mathrm{Cost}(y_{1}; u) = \frac12(y_{1} - u)^{2}$; for any $s > 1$ and for all $u$,

For each $u$, this recursion encapsulates two possibilities: (i) there is no changepoint at the $(s-1)$st timepoint, and the optimal cost is equal to the previous cost plus the cost of a new data point, $\mathrm{Cost}(y_{1:(s-1)};u) + \frac12(y_{s} - u)^{2}$; (ii) there is a changepoint at the $(s-1)$st timepoint, and the optimal cost is equal to the optimal cost of segmenting up to $s-1$ plus the penalty for adding a changepoint at $s-1$ plus the cost of a new data point, $\min_{u’}{\mathrm{Cost}(y_{1:(s-1)};u’)} + \lambda + \frac12(y_{s} - u)^{2}$.

Setting functional_pruning_out = TRUE allows us to examine $\mathrm{Cost}(y_{1:s}; u)$. The following plots $\mathrm{Cost}(y_{1:300}; u)$. Colors represent the most recent changepoint associated with optimal cost at each $u$.

lam <- 4
fit <- changepoint_estimates(dat, "L0", lam, functional_pruning_out = TRUE)
p <- plot(fit, s = 300)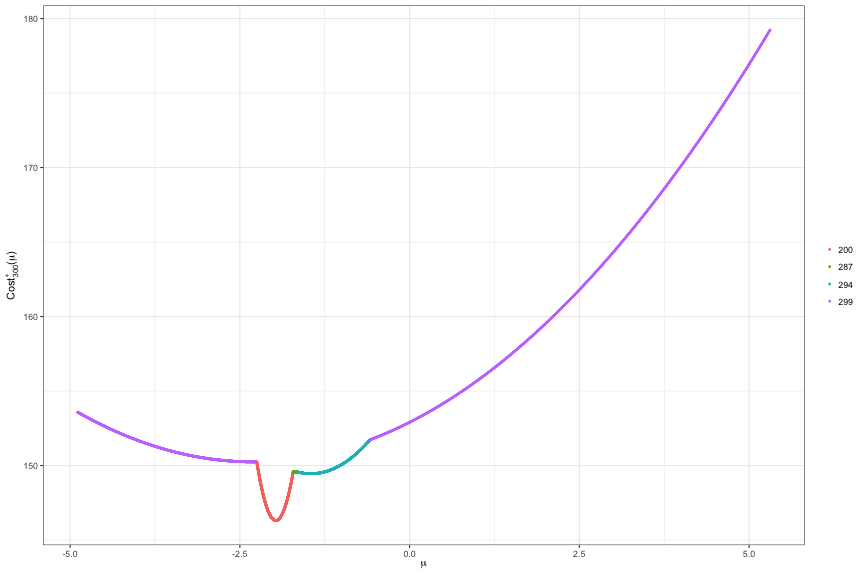

plot of chunk unnamed-chunk-3

To manually access the cost functions use fit$piecewise_square_losses. Since $\mathrm{Cost}(y_{1:s}; u)$ is piecewise quadratic, we represent each component through its coefficients (square, linear, constant) over domain (min_mean, max_mean). Furthermore, we store the most recent changepoint data_i for each region (min_mean, max_mean).

For example, the plot above is created by filtering the dataframe to $s = 300$. We see that this cost function is defined over five regions with most recent changepoints at 200, 287, 294, 299.

fit$piecewise_square_losses[fit$piecewise_square_losses$s == 300, ]
##      square     linear constant   min_mean   max_mean prev_last_mean
## 1617    0.5   2.305815 152.9045 -4.8889207 -2.2512053      -1.966938
## 1618   50.0 197.032646 340.4123 -2.2512053 -1.7139801       2.962192
## 1619    6.5  21.534563 167.4032 -1.7139801 -1.6503894      -2.017219
## 1620    3.0   8.722768 155.7920 -1.6503894 -0.5818996      -2.003297
## 1621    0.5   2.305815 152.9045 -0.5818996  5.3079784      -1.966938
##      data_i   s
## 1617    299 300
## 1618    200 300
## 1619    287 300
## 1620    294 300
## 1621    299 300

Changepoint inference

The conditioning set $\mathcal{S}$ can be extracted for fixed and adaptive $\nu$s by setting return_conditioning_sets = TRUE. See Section 3 of our paper (Jewell, Fearnhead, & Witten, 2019) for additional details.

For example,

h <- 10
K <- 2
fit_inference <- changepoint_inference(dat, 'BS-fixed', K, window_size = h, sig = 1, return_conditioning_sets = TRUE)

The conditioning set for each estimated changepoint can be accessed through

fit_inference$conditioning_sets
## [[1]]
##     min_mean   max_mean contained
## 1       -Inf -63.819416         1
## 2 -63.819416  -1.555879         1
## 3  -1.555879  33.068620         0
## 4  33.068620        Inf         1
## 
## [[2]]
##    min_mean  max_mean contained
## 1      -Inf -8.835202         1
## 2 -8.835202  2.720512         0
## 3  2.720512 13.128808         1
## 4 13.128808       Inf         1

Each row is a subset of $\mathbb{R}$ defined as (min_mean, max_mean). This region is in $\mathcal{S}$ if contained = 1.

There are simple plotting tools to visualize these sets:

plot(fit_inference, thj = fit_inference$change_pts[1])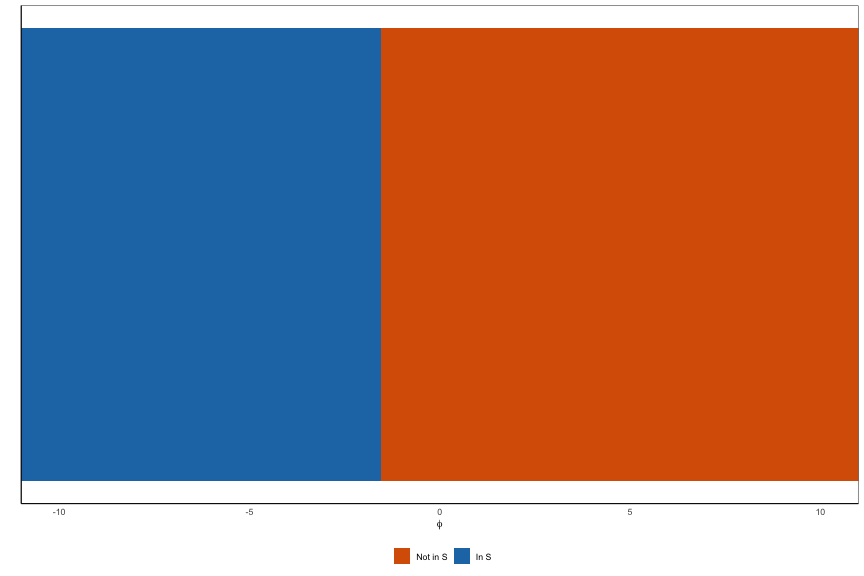

plot of chunk unnamed-chunk-7

In the case of inference with $\ell_0$ segmentation, it is also possible to view the cost of segmenting the data as a function of $\phi$, that is,

fit_inference <- changepoint_inference(dat, 'L0-fixed', lam, window_size = h, sig = 1, return_conditioning_sets = TRUE)
plot(fit_inference, thj = fit_inference$change_pts[1])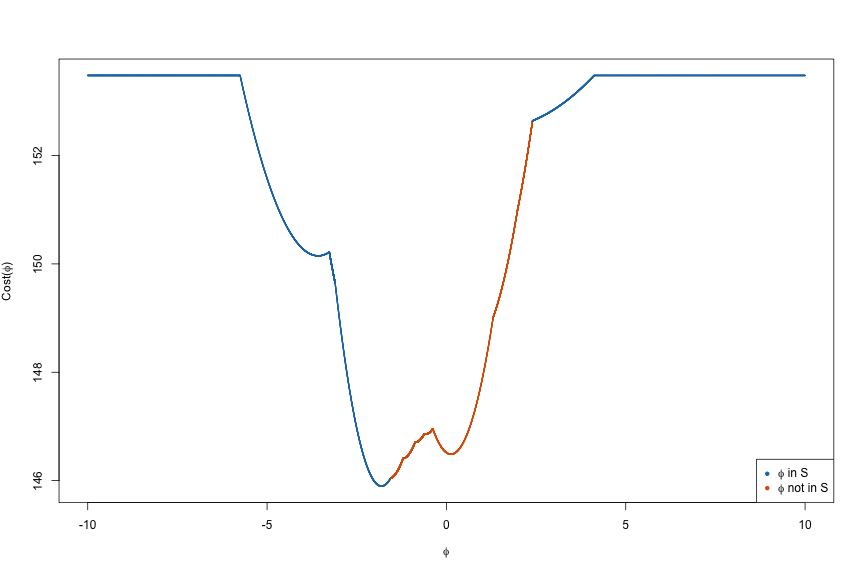

plot of chunk unnamed-chunk-8

References

  1. Rigaill, G. (2015). A pruned dynamic programming algorithm to recover the best segmentations with 1 to K_max change-points. Journal De La Société Française De Statistique, 156(4), 180–205.
  2. Maidstone, R., Hocking, T., Rigaill, G., & Fearnhead, P. (2017). On optimal multiple changepoint algorithms for large data. Statistics and Computing, 27(2), 519–533.
  3. Jewell, S., Fearnhead, P., & Witten, D. (2019). Testing for a change in mean after changepoint detection. ArXiv Preprint ArXiv:1910.04291.